Proceedings of the 20th Meeting of the Cognitive Science Society. (pp. 398-403). Mahwah, NJ: Erlbaum.

(c) Cognitive Science Society

EPAM (Elementary Perceiver And Memorizer) is a cognitive architecture first developed by Feigenbaum and Simon in the early sixties. At its core lie mechanisms for encoding chunks into long-term memory (LTM) through the construction of a discrimination net and mechanisms for handling information in short-term memory (STM). EPAM was originally built to provide a unifying theory of verbal behavior (Feigenbaum & Simon, 1962, 1984), was later used for simulating chess memory (Simon & Gilmartin 1973), and has recently been applied to letter perception and expert digit-span memory (Richman & Simon, 1989; Richman, Staszewski & Simon 1995). Although not yet as influential as Soar (Newell, 1990) or ACT-R (Anderson, 1993), EPAM remains attractive as a parsimonious, chunk-based explanation for perceptual and memory phenomena. As added value, EPAM addresses phenomena that are not yet accounted for by Soar and ACT-R and may offer a useful extension of these theories.

In this paper, I focus on chess memory and use CHREST (for Chunk Hierarchy and REtrieval STructure; see De Groot & Gobet, 1996, and, Gobet, 1993a, b, for earlier accounts of the model), an expansion of Simon and Gilmartin’s (1973) MAPP program, itself a program inspired by EPAM. After discussing the advantages of chess as a research domain, I present some data from chess memory experiments, with a special emphasis on the recall of random positions. These data are used to compare some leading theories in the field of expertise. I then describe CHREST in some detail and compare its behavior with that of humans in experiments where random positions are presented for durations between one and sixty seconds. Finally, I discuss to what extent the EPAM architecture can be used with visuo-spatial tasks.

How can we explain this popularity? As argued elsewhere (Gobet, 1993b), several factors speak in favor of chess. To begin with, chess is a complex and challenging domain, while, at the same time, allowing a clean formal description that makes it relatively easy to develop mathematical and computational models. In addition, chess has good ecological validity (Neisser, 1976), allowing one to study experts in their usual environment. As a consequence, many experimental manipulations are possible which are still close enough to the "real thing" to ensure that chess players are highly motivated. Moreover, the Elo rating 1 (Elo, 1978) offers a quantitative scale of measurement widely used in the chess community that provides the researcher with a fine-grained classification. This makes it possible both to use statistical techniques like regression analysis and to meaningfully compare samples from different studies. Just think of domains such as medical or physics expertise, where participants are typically classified into three groups (novices, intermediates, and experts), which are hard to compare from one study to another, and you will readily realize the advantage offered by chess and its rating system. Finally, chess is a natural domain to consider for developing a computational model of cognition, because a large body of empirical data on chess expertise already exists (see Holding, 1985, or Gobet, 1993b, for reviews).

Much of what is known about chess expertise goes back to De Groot’s seminal work (1946/1978). One of De Groot’s important findings was that there are clear differences in a memory task consisting in the brief presentation of a position taken from a tournament game. Typically, players at and above master level recall the entire position almost perfectly, while weaker players are overwhelmed by the task (see Figure 2 below). A natural extension of De Groot’s work was to ask chessplayers to recall meaningless positions (see Figure 1 for examples of game and random position). This was first carried out in 1964 in Amsterdam by De Groot and his students, who found that players of all skill levels were identically poor at recalling meaningless positions. Interestingly, they considered this result so obvious and trivial that it did not deserve publication (Vicente & De Groot, 1990). It was only in 1973 that a replication was carried out (and published) by Chase and Simon, who extended the Amsterdam work both experimentally, by adding a copy task to the memory task, and theoretically, by developing what is commonly known as the "chunking theory" (Chase & Simon, 1973; Simon & Chase, 1973).

Figure 1: Types of positions typically used in chess research on memory. On the left, a game position taken from a tournament game. On the right, a random position obtained by shuffling the piece locations of a game position.

The use of meaningless material had two functions. First, it served as a control condition for ruling out the possibility that chess masters were performing better just because of superior mental abilities. Second, it addressed one of the challenges of cognitive science, which is, to put it simply, to tease apart architectural components (the "hardware") from knowledge components (the "software"). The idea is that, because knowledge structures are of little use in the case of random positions, this type of material offers a baseline condition with which knowledge-rich stimuli may be compared. As is clear from research in neuropsychology and in developmental psychology, this approach contains many pitfalls, including the fact that the hardware/software dichotomy may represent quite a simplification and may collapse several levels of processing.

Like the unpublished data collected by De Groot and his colleagues, the data obtained by Chase and Simon with random positions were reassuring: there was no difference in recall between their three subjects, a master, a class A player, and a novice. Taken together with grandmasters’ and masters’ massive recall superiority with game positions over weaker players, the uniform poor recall with random positions was such a vivid illustration of the principle that knowledge is the key to expertise that it has become a classic finding, widely cited in textbooks of cognitive psychology and in papers on expertise. There is no doubt that the random position experiment contributed to making Chase and Simon’s papers "classics" in the field (Charness, 1992).

As usual, things are more complicated than the textbook account. When Herb Simon and I were working on CHREST, a re-implementation and extension of MAPP (Simon & Gilmartin 1973), a program aimed at simulating chess memory, it occurred to us that the model was making predictions about the recall of random positions that were at variance with the classical no-skill-difference result. As will be described later in more detail, CHREST constructs a discrimination net of chunks by scanning positions from a database of master games and identifying patterns of pieces in these positions. As expected, the model was getting better and better at remembering game positions as the number and the average size of its chunks increased. However, the model was also showing a small, but robust increase in recall with random positions. This was a matter of serious concern, for it was clear that the simulations were correct and that the skill differences in recall were due to a simple mechanism: just by chance, it is more likely for a large discrimination net than for a small one that chunks could be found in random positions. We therefore decided to do a systematic review of experiments using random positions. Altogether, we found 13 studies (Gobet & Simon, 1996a). In 12 of them, masters did maintain some advantage, even if

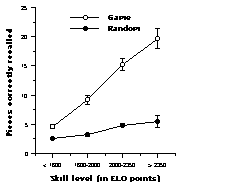
Figure 2: Mean number (averaged over 13 studies) of pieces placed correctly as a function of position type (game or random) and skill level. Positions had 25 pieces on average, and the presentation time was ¾ 10 s. Error bars indicate standard errors of the means. After Gobet and Simon, 1996a.

it was less impressive than with game positions. The only exception was Chase and Simon’s (1973) study, where the master actually did worse than the novice! While the skill differences were not significant in most studies because of lack of statistical power, it became clear that the effect was genuine when the various studies were pooled together (see Figure 2).

Our first reaction was to conclude that random positions do not offer the kind of control stimuli hoped for. This is certainly an annoyance for the field, but not as bad as might be feared, as independent evidence shows that there is no correlation between chess skill and general cognitive abilities, including visual memory for non-domain-specific material (Gobet & Simon, 1996a; Holding, 1985). Our second reaction was to realize that random positions offer a powerful way of teasing apart current theories of chess expertise. A comparison of four theories of chess skill (Gobet, in press), shows that two of them, the chunking theory (Chase & Simon, 1973), and the template theory (Gobet & Simon, 1996b), an extension of the chunking theory, predict masters’ superiority with random positions. It also shows that two other approaches, the long-term working memory theory (Ericsson & Kintsch, 1995) and Holding’s (1985) SEEK theory do not account for the result, the former because it overestimates recall performance with random positions, and the latter, which emphasizes the role of high-level, conceptual knowledge, because it underestimates performance.

As mentioned above, the chunking theory proposes that expertise in a domain develops by the creation of a discrimination net, through which stimuli can be rapidly recognized. With learning, individual features or parts of stimuli are chunked, which allows a more efficient storage of the information in short-term memory (STM). Now and then, masters adventitiously recognize chunks in random positions, which explains their superiority with this type of material. The template theory adds to this view the idea that chunks that recur often in the domain of expertise develop into larger and more complex structures (templates), which have slots that allow values of variables to be stored rapidly. Templates are related to retrieval structures, which play an important role in the skilled memory theory (Chase & Ericsson, 1982) and in its extension, the long-term working memory theory (Ericsson & Kintsch, 1995). The difference is that the latter theories propose a general, multi-purpose retrieval structure, while the template theory proposes several, specific structures that may be used only after they have been accessed by recognition processes. Since templates contain large chunks, their access conditions are unlikely to be met in random positions. On the other hand, the retrieval structure proposed by Ericsson and Kintsch can be used even with random positions; hence their incorrect predictions that masters can store information from random positions rapidly.

The skill difference in recalling random positions indicates that this material does not tap hardware variables alone. However, because the amount of knowledge used is low, this material still offers a reasonable solution for reaching tentative conclusions about the hardware of the cognitive system and, therefore, for testing some of the system constants proposed in the EPAM theory (Feigenbaum & Simon, 1984), from which both the chunking and template theories stem. The template theory has been implemented in the latest version of CHREST. Simulations show that templates are almost never accessed with random positions, because the conditions of their evocation are not met. Without templates, the current implementation is close enough to the specifications of the chunking theory to allow us to study the template and chunking theories together.

The model consists of the following components: recognition LTM, semantic LTM, and STM. STM is made of 2-5 visual chunks (simulations presented later will explore the effect of varying STM size). STM is a queue, with the exception of the largest chunk met at any point in time (the "hypothesis"), which is kept in STM until a larger chunk is met. Figure 3 presents an overview of the model.

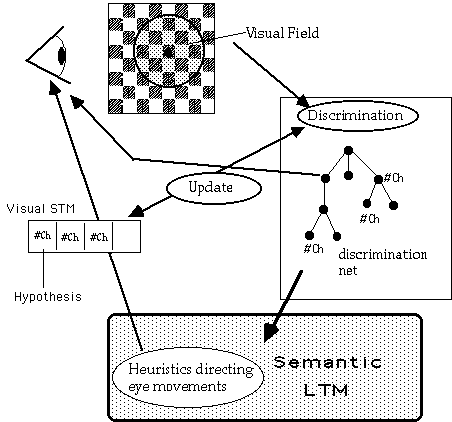
Figure 3: Overview of CHREST (#Ch stands for Chunk).

Attention is modeled by eye movements (see Chapter 8 of De Groot & Gobet, 1996, for more about mechanisms directing eye movements). For each new fixation, the model sorts the pieces found in the visual space through the discrimination net. (The visual space is defined as the squares located at most two squares away from the fixation point.) Learning new chunks essentially occurs in the same way as in the EPAM model, with the qualification that only one type of (implicit) test is carried out in CHREST: "What is the next item in the visual space?", while EPAM allows for testing various features of objects. The uniformity of tests has been adopted in order to grow large nets; it is assumed that other tests in addition to the location of pieces are carried out by human players, such as tests dealing with threats, plans, and other concepts.

The net is grown by two learning mechanisms, familiarization and discrimination. When a new object is presented to the model, it is sorted through the discrimination net. When a node is reached, the object is compared with the image of the node, which is the internal representation of the object. If the image under-represents the object, new features are added to the image (familiarization). If the information in the image and the object differ on some feature or some sub-element, a new node is created (discrimination).

Two other learning mechanisms (one for creating templates and the other for creating links between nodes) will not be described here, since these features of the program are almost never relevant with random positions.

In order to test the plausibility of the parameters used in CHREST, Gobet and Simon (1995) collected data from random and game positions where the presentation time was systematically varied from 1 s to 60 s. Data are based on 20 subjects: 5 grand or international masters (mean Elo=2498), 8 experts (mean Elo=2121), and 7 class A players (mean Elo=1879). Positions for the random condition were created by randomly placing pieces from a game position on the chessboard, and were presented to subjects on a computer screen. For the random condition, in which we are interested here, one position was presented for each of the following times: 1, 2, 3, 4, 5, 10, 20, 30, and 60 s. The results are given in Figures 4 to 6 (thick lines).

Three nets, having 1,000, 10,000, and 100,000 nodes (referred to below as, respectively, 1k, 10k and 100k nets) were created by letting the program scan a database of several thousand positions. The sizes of the three nets were chosen in order to have nets of three different orders of magnitude. The matching between the three nets and levels of expertise (class A players, experts, and masters respectively) was rather loose and based on earlier simulations. For ease of exposition, I will directly compare these 1k, 10k, and 100k programs with class A, experts, and masters, respectively. The reader should, however, keep in mind that this is only an approximation.

Twenty random positions were presented for each of the presentation times. For each position, CHREST moved its simulated eyes around the board, storing recognized chunks into STM, and, when applicable, using the following learning mechanisms. First, as described before, CHREST chunks two chunks together (that is, adds a chunk as a test to another chunk). It takes 8 seconds to carry out this discrimination operation, as in the EPAM theory (see Simon, 1976, for a discussion of this parameter). Typically, a new test is added to the hypothesis. Second, chunks that have been in STM for at least 4 seconds are "flagged," which means that episodic cues that permit the access to this node are added to the discrimination net. Flagging is a type of familiarization. Little is said in the EPAM theory about the time needed to familiarize a node, except that this operation is faster than discrimination. This value has arbitrarily been set to 4 s in CHREST. Flagged nodes can be recalled during the reconstruction phase even if they are no longer in STM.

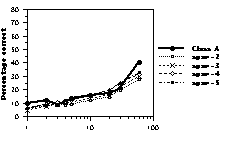
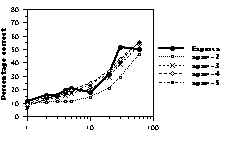
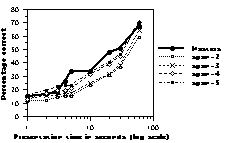
Figure 4: Percentage correct as a function of presentation time. Thick lines represent human data. Dotted lines represent CHREST simulations with 1k nodes (upper panel), 10k nodes (middle panel), and 100k nodes (lower panel) with STM spans ranging from 2 to 5.

The following parameters were used during the simulations (see De Groot & Gobet, 1996, for the parameters related to eye movements):

• time to create a chunk in LTM 8 s

• time to flag a node 4 s

• time to place a symbol into STM 50 ms

• time to compare two symbols 50 ms

• time to carry out a test in the net 10 ms

The three versions of the program were used with 4 different STM capacity parameters (from 2 to 5 slots).

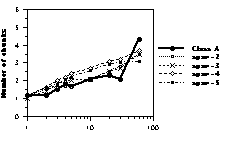
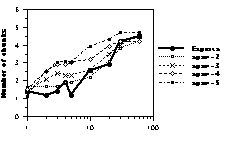
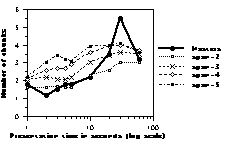
Figure 5: Number of chunks as a function of presentation time. Thick lines represent human data. Dotted lines represent CHREST simulations with 1k nodes (upper panel), 10k nodes (middle panel), and 100k nodes (lower panel) with STM spans from 2 to 5.

When presentation times equal or less than 10 seconds are pooled, Gobet and Simon’s (1995) recall percentages (Class A: 11.7%, experts: 17.0%, masters: 23.7%) show the same pattern illustrated in Figure 2. Run on the positions used by Gobet and Simon (1995), CHREST simulates the skill effect with random positions, though the percentage of recall is somewhat less than with humans. With a STM span of 4 slots, the 1k, 10k and 100k nets obtained performance of 10.5%, 15.6%, and 20.3%, respectively.

Percentage Correct The results on percentage correct are

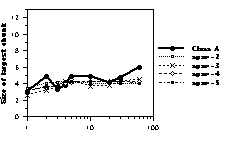
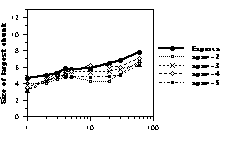
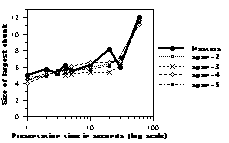
Figure 6: Size of the largest chunk as a function of presentation time. Thick lines represent human data. Dotted lines represent CHREST simulations with 1k nodes (upper panel), 10k nodes (middle panel), and 100k nodes (lower panel) with STM spans from 2 to 5.

illustrated in Figure 4. Larger spans allow better recall, though the effect is not as large as one might have expected. This is due to the fact that chunks stored in STM or LTM overlap, and, as a consequence, additional chunks bring less and less new information. The model matches the human data well for the three skill levels. The class A and expert programs are slightly below human performance with one and two seconds. It is possible that humans perceive configurations according to Gestalt rules that are not captured by the way chunks are stored in the program. Additional time allows more chunks to be found and compensates for this.

Number of Chunks With humans, chunks are defined as sequences of pieces having latencies of less than 2 seconds between successive pieces. Pieces placed individually are not counted as chunks, as they are often due more to guessing than to memory. (The number of chunks for humans is thus slightly underestimated.) As for CHREST, it sequentially replaces the pieces contained in the nodes held in STM or accessible from LTM through episodic cues. Such nodes are counted as chunks only if they contain at least one piece not already replaced. Obviously, the number of chunks stored increases with STM span. Overall, the programs with a small STM span obtain a number of chunks similar to that of human players (Figure 5).

Size of the Largest Chunk In general, the largest chunk output by the program is slightly smaller than human players’ (Figure 6), though the fit gets better with the master version. The correlation between STM span and size of the largest chunk is rather low (0.20, 0.27, 0.03, for the 1k, 10k, and 100k versions of the program).

In summary, the simulations show that CHREST, using several parameters from the EPAM theory, successfully accounts for the role of presentation time in the recall of random chess positions. Given that most of the EPAM applications were done with verbal material (see Feigenbaum & Simon, 1984), it was important to show that EPAM parameters are plausible with visuo-spatial material as well.

Three sets of mechanisms were crucial for the success of the simulations: (a) mechanisms allowing chunks to be rapidly recognized and sorted by the discrimination net; (b) mechanisms allowing chunks to be created or tagged when the presentation time is sufficiently long; and (c) mechanisms directing the attention of the program. Finally, the results are consistent with the estimate that visuo-spatial STM contains 3 or 4 chunks (Zhang & Simon, 1985).

In spite of its checkered history, the technique of using random chess positions has provided a powerful tool for testing theories of chess memory. It remains to be seen whether similar techniques can show such a discriminative power in other domains of expertise as well.

I am grateful to Herb Simon for his involvement in many aspects of this research and to Julian Pine and Frank Ritter for comments on this paper.

FootNotes

1 The Elo rating scale is an interval scale ranking competitive chess players, with a standard deviation of 200. Skill levels have standard names, which are used consistently in this paper (in parentheses, the corresponding range in Elo points): grandmaster (above 2500), international master (2400-2500), master (2200-2400), expert (2000-2200), class A players (1800-2000), class B players (1600-1800), and so on. Back to Main Text